Terugblikken en vooruitkijken
Het weerstation P41_Ermelo functioneert nu meer dan een jaar en genereert elk tien minuten data over het weer. Via de website van weathercloud.net zijn de data over een langere periode op te vragen. Aan de hand van de maand- en jaaroverzichten is inmiddels een dataset aangelegd van 4 december 2020 tot en met 21 februari 2022. Deze informatie geeft een gedetailleerd inzicht in de ontwikkelingen van het weer in het verleden. Zou het ook mogelijk zijn om met deze data het weer te voorspellen?
Tijdreeksanalyse
In een eerder bericht dat verschenen is over het werken met weerdata in python, is de code toegelicht aan de hand waarvan de maandoverzichten op deze site gerapporteerd worden. In dit bericht gaan we verder in op het uitvoeren van tijdreeks analyses om het weer te voorspellen. De data uit het verleden bieden informatie over de ontwikkeling (van een bepaalde variabele) in de toekomst. Een tijdreeksmodel zal in het algemeen waarnemingen in de nabije toekomst beter voorspellen dan waarnemingen verder weg in de toekomst.
Modellen voor tijdreeksgegevens kunnen vele vormen aannemen en vertegenwoordigen verschillende stochastische processen. Bij het modelleren van schommelingen in het niveau van een proces, zijn drie categorieën van praktisch belang, namelijk de autoregressieve (AR)-modellen, de geïntegreerde (I) modellen, en de voortschrijdend gemiddelde (MA) modellen.
ARIMA model
Het Autoregressive Integrated Moving Average (ARIMA) model staat voor een tijdreeksmodel dat gegevens uit het verleden gebruikt om de gegevens te interpreteren en voorspellingen te doen. Het ARIMA-model maakt gebruik van lineaire regressie. Het is een populaire en veelvuldig toegepaste statistische methode voor tijdreeksanalyses. Het is bijvoorbeeld te gebruiken voor het voorspellen van prijzen op basis van historische verdiensten. Univariate modellen zoals het ARIMA model zijn nuttig om de temperatuur te voorspellen. Het is ook mogelijk om seizoenspatronen mee te nemen in de voorspelling, maar dat komt in een volgend bericht aan de orde. Het ARIMA model wordt beschreven met drie parameters met dank aan de beschrijving van livingeconomyadvisors.
- De term ‘AR’ in ARIMA staat voor autoregressie, wat aangeeft dat het model de afhankelijke relatie gebruikt tussen huidige gegevens en eerdere waarden. Met andere woorden, het laat zien dat de gegevens worden teruggebracht op de waarden uit het verleden.
- De term ‘I’ staat voor geïntegreerd, wat betekent dat de gegevens stationair zijn. Stationaire gegevens verwijzen naar tijdreeksgegevens die “stationair” zijn gemaakt door de waarnemingen af te trekken van de vorige waarden.
- De term ‘MA’ staat voor moving average model, wat aangeeft dat de voorspelling of uitkomst van het model lineair afhangt van de waarden uit het verleden. Het betekent ook dat de fouten in prognoses lineaire functies zijn van fouten uit het verleden.
Deze termen worden in de standaard notatie voor ARIMA met drie parameters aangeduid
De parameters p, d en q
- De parameter p is het aantal autoregressieve termen of het aantal ‘vertragingswaarnemingen’. Het wordt ook wel de “lag-order” genoemd en het bepaalt de uitkomst van het model door vertraagde datapunten te leveren.
- De parameter d staat bekend als de mate van differentiëren. het geeft aan hoe vaak de vertraagde indicatoren zijn afgetrokken om de gegevens stationair te maken.
- De parameter q is het aantal voorspellingsfouten in het model en wordt ook wel de grootte van het voortschrijdend-gemiddelde-venster genoemd.
De parameters hebben de waarde van gehele getallen en moeten worden gedefinieerd om het model te laten werken. Ze kunnen ook de waarde 0 hebben, wat inhoudt dat ze niet in het model zullen worden gebruikt. Op deze manier kan het ARIMA-model worden omgezet in:
- ARMA-model (geen stationaire gegevens, d = 0 )
- AR-model (geen voortschrijdende gemiddelden of stationaire gegevens, alleen een autoregressie op eerdere waarden, d = 0, q = 0 )
- MA-model (een voortschrijdend-gemiddelde-model zonder autoregressie of stationaire gegevens, p = 0, d = 0)
Daarom kunnen ARIMA-modellen worden gedefinieerd als:
- ARIMA (1, 0, 0) – bekend als het autoregressieve model van de eerste orde
- ARIMA (0, 1, 0) – bekend als het random walk-model
- ARIMA (1, 1, 0) – bekend als het gedifferentieerde eerste-orde autoregressieve model , enzovoort.
Zodra de parameters ( p, d, q ) zijn gedefinieerd, beoogt het ARIMA-model coëfficiënten te schatten op basis waarvan de tijdreeks zo goed mogelijk kan worden geschat.
Zijn de data stationair?
Het ARIMA model werkt op basis van de veronderstelling dat de data stationair zijn. De parameters zoals het gemiddelde en de variantie veranderen dan niet in de loop van de tijd. Vergelijk het met een (ideale) slinger waarvan de amplitude en de frequentie constant blijft. Laten we kijken naar een tijdreeksanalyse van de temperatuur en of deze analyse voldoende handvatten biedt voor een betrouwbare voorspelling.
Importeer de benodigde libraries in python
import pandas as pd
import requests, json, datetime
import matplotlib.pyplot as plt
import numpy as np
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima_model import ARIMAResults
from sklearn import metrics
from timeit import default_timer as timer
import warnings
warnings.filterwarnings("ignore")
import math
Lees de dataset in en print deze uit (eerste vijf en laatste vijf regels van het dataframe). Naast temperatuurdata bevat de dataset data over de luchtdruk, de neerslag en de opgewekte (zonne-)energie. Aangezien we ons voor nu richten op een univariate tijdreeksanalyse, zijn de laatste drie data-attributen voor deze tijdreeksanalyse niet nodig. Bij het toepassen van een multivariate analyse kunnen deze data wel van pas komen.
df = pd.read_csv('C:/pad/weer_cum.csv', delimiter=';', header=0, parse_dates=True, infer_datetime_format=True, dayfirst=True, decimal=',', thousands='.')
print(df)
datum minimumtemp min_druk min_neerslag gemiddelde_temp \
0 04-12-2020 0.5 982.7 2.0 5.1
1 05-12-2020 -1.0 991.5 0.0 1.6
2 06-12-2020 -0.7 998.2 0.0 2.0
3 07-12-2020 2.3 994.6 0.0 4.7
4 08-12-2020 0.0 1001.7 0.0 2.5
.. ... ... ... ... ...
440 17-02-2022 5.2 990.2 0.0 8.8
441 18-02-2022 4.6 986.6 0.0 7.6
442 19-02-2022 3.5 999.0 0.0 5.7
443 20-02-2022 3.9 988.2 0.0 7.5
444 21-02-2022 3.4 991.9 0.0 5.4
gem_druk gem_neerslag maximumtemp energie max_druk max_neerslag
0 987.2 2.0 8.3 NaN 991.0 2.0
1 997.0 0.0 5.3 2286.0 1002.5 0.0
2 1001.4 0.3 5.1 1336.0 1002.7 1.2
3 997.5 7.5 5.9 732.0 1001.6 10.4
4 1004.5 0.0 4.9 1173.0 1007.8 0.0
.. ... ... ... ... ... ...
440 1001.1 2.1 11.2 5489.0 1009.8 3.2
441 998.0 2.4 11.3 5489.0 1010.0 10.4
442 1007.2 1.9 8.2 5489.0 1012.5 13.2
443 1001.5 12.3 10.0 4485.0 1010.3 38.8
444 995.5 0.4 6.3 4485.0 996.7 2.0
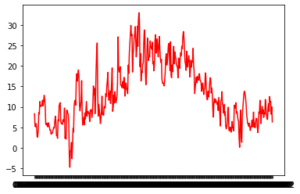
Aangezien de data nog niet meerdere seizoenen (jaren) beslaan, is de vraag of de data stationair zijn, lastig te beantwoorden. Eigenlijk moet de dataset meerdere jaren omvatten. Er zijn statistische testen die aantonen of de data stationair zijn of niet. De Dickey-Fuller test passen we hieronder toe. Om vast te stellen dat de tijdreeks stationair is, moet de nul hyopthese worden verworpen. Deze hypothese houdt in dat een unit root in de data aanwezig is. indien de alternatieve hypothese wordt aangenomen, dan zijn de data stationair. We gebruiken een significantieniveau van 5% om de nul hypothese te testen.
def adf_test(dataset): # definieer de functie om de dickey-fuller test uit te voeren adftest = adfuller(dataset, autolag = 'AIC')
print("1. ADF : ",dftest[0])
print("2. P-Value : ", dftest[1])
print("3. Num Of Lags : ", dftest[2])
print("4. Num Of Observations Used For ADF Regression and Critical Values Calculation :", dftest[3])
print("5. Critical Values :")
for key, val in adftest[4].items():
print("\t",key, ": ", val) # druk de analyse met de key parameters af
#toon de resultaten voor de gemiddelde temperatuur
adf_test(df['gemiddelde_temp'])
#toon de resultaten voor de maximumtemperatuur
adf_test(df['maximumtemp'])
#toon de resultaten voor de maximumtemperatuur
adf_test(df['minimumtemp'])
gemiddelde temperatuur 1. ADF : -1.3737768089727267 2. P-Value : 0.5947812974352094 3. Num Of Lags : 13 4. Num Of Observations Used For ADF Regression and Critical Values Calculation : 410 5. Critical Values : 1% : -3.4464005219454155 5% : -2.868615280538588 10% : -2.570538905413444 maximum temperatuur 1. ADF : -2.8622137038678708 2. P-Value : 0.04992178061500779 3. Num Of Lags : 3 4. Num Of Observations Used For ADF Regression and Critical Values Calculation : 420 5. Critical Values : 1% : -3.4460159927788574 5% : -2.868446209372638 10% : -2.570448781179138 minimumtemperatuur 1. ADF : -1.5096079066231929 2. P-Value : 0.5287532038695358 3. Num Of Lags : 13 4. Num Of Observations Used For ADF Regression and Critical Values Calculation : 410 5. Critical Values : 1% : -3.4464005219454155 5% : -2.868615280538588 10% : -2.570538905413444
Alleen voor de maximumtemperatuur is de p-waarde kleiner dan 5% (groen gemarkeerd). We kunnen de alternatieve hypothese aannemen dat de maximumtemperatuur stationair is. Dat geldt niet voor de gemiddelde en minimumtemperatuur (rood gemarkeerd(. We nemen voor de tijdreeksanalyse de maximumtemperatuur als uitgangspunt.
Beperk de dataset tot enkel de datum en de maximumtemperatuur
df = df.loc[:,['datum', 'maximumtemp']]
print(df.head())
Maak de kolom datum tot index van het dataframe
df.set_index('datum',inplace=True) #maak de kolom dag tot index en vervang deze in het dataframe
Splits de dataset in een trainingset en een testset. Gebruikelijk is een verhouding van 70% à 80% om het model te trainen en 20% à 30% om het model te testen. In deze test komt 30% overeen met de laatste 101 rijen van het dataframe die zullen worden gebruikt om het model te testen.
train=df.iloc[:-101]
test=df.iloc[-101:]
print(train.shape,test.shape)
print(train.tail())
print(test.head())
y = train['maximumtemp']
Test het ARIMA model voor bepaalde parameters
Het ARIMA model wordt getest bij parameter waarden p = 2, d = 3, q = 2. Dit zijn willekeurige waarden om te kijken hoe het model werkt. Later zullen we de parameter waarden optimaliseren.
# Autoregressive Integrated Moving Average (ARIMA)
# voorbeeld bij p = 2, d = 3, q = 2
ARIMAmodel = ARIMA(y, order = (2, 3, 2))
ARIMAmodel = ARIMAmodel.fit()z_pred = ARIMAmodel.get_forecast(len(test.index))
z_pred_df = z_pred.conf_int(alpha = 0.05)
z_pred_df["Predictions"] = ARIMAmodel.predict(start = z_pred_df.index[0], end = z_pred_df.index[-1])
z_pred_df.index = test.index
z_pred_out = z_pred_df["Voorspellingen"]
plt.plot(z_pred_out, color='Yellow', label = 'ARIMA Voorspellingen')
plt.legend()
Bepaal de root mean square error (RMSE), de gemiddelde standaardafwijking, tussen de voorspelde temperatuur en de gemeten temperatuur. Hoe lager de RMSE waarde, hoe beter het model voorspelt. De afwijking is nog best groot met 3,2 °C.
arma_rmse = np.sqrt(mean_squared_error(test["maximumtemp"].values, z_pred_df["Voorspellingen"]))
print("RMSE: ",arma_rmse)
RMSE: 3.2873659467946212

Test de RMSE bij verschillende parameters
def forecast(p,d,q):
ARIMAmodel = ARIMA(y, order = (p, d, q))
ARIMAmodel = ARIMAmodel.fit()
z_pred = ARIMAmodel.get_forecast(len(test.index))
z_pred_df = z_pred.conf_int(alpha = 0.05)
z_pred_df["Voorspellingen"] = ARIMAmodel.predict(start = z_pred_df.index[0], end = z_pred_df.index[-1])
z_pred_df.index = test.index
z_pred_out = z_pred_df["voorspellingen"]
#plt.plot(z_pred_out, color='Red', label = 'voorspellingen')
arma_rmse = np.sqrt(mean_squared_error(test["maximumtemp"].values, z_pred_df["voorspellingen"]))
print("bij p=",p, ", d=",d, " en q=",q, "is RMSE gelijk aan: ",arma_rmse)
return arma_rmseParameters = []
X = range(1,3)
for p in X:
for d in X:
for q in X:
Parameters.append(forecast(p,d,q))print("De lijst met p-, d- en q-waarden geeft volgende RMSE :", Parameters)
bij p= 1 , d= 1 en q= 1 is RMSE gelijk aan: 7.990294983659258 bij p= 1 , d= 1 en q= 2 is RMSE gelijk aan: 7.8672325533189325 bij p= 1 , d= 2 en q= 1 is RMSE gelijk aan: 5.632543662520966 bij p= 1 , d= 2 en q= 2 is RMSE gelijk aan: 5.313728799948607 bij p= 2 , d= 1 en q= 1 is RMSE gelijk aan: 7.84017358830696 bij p= 2 , d= 1 en q= 2 is RMSE gelijk aan: 7.819040996395016 bij p= 2 , d= 2 en q= 1 is RMSE gelijk aan: 6.191112879889703 bij p= 2 , d= 2 en q= 2 is RMSE gelijk aan: 5.434140094607043 De lijst met p-, d- en q-waarden geeft volgende RMSE : [7.990294983659258, 7.8672325533189325, 5.632543662520966, 5.313728799948607, 7.84017358830696, 7.819040996395016, 6.191112879889703, 5.434140094607043]
Bepaal een matrix met de bandbreedte voor elke parameter waarde p, d en q
parameters = pd.DataFrame(columns=['P', 'D', 'Q'])
def frame_vullen(i,j,k):
parameters.loc[len(parameters.index)] = [k,j,i]
X = range(1,5)
for k in X:
for j in X:
for i in X:
frame_vullen(i,j,k)
parameters['RMSE'] = 0
print(parameters)
P D Q RMSE 0 1 1 1 0 1 1 1 2 0 2 1 1 3 0 3 1 1 4 0 4 1 2 1 0 .. .. .. .. ... 59 4 3 4 0 60 4 4 1 0 61 4 4 2 0 62 4 4 3 0 63 4 4 4 0 [64 rows x 4 columns]
Bereken de RMSE voor elke set van p, d en q
for item in parameters.index:
p = parameters.loc[item,'P']
d = parameters.loc[item,'D']
q = parameters.loc[item,'Q']
parameters.loc[item,'RMSE'] = forecast(p,d,q)print(parameters)
bij p= 1 , d= 1 en q= 1 is RMSE gelijk aan: 7.990295032280518 bij p= 1 , d= 1 en q= 2 is RMSE gelijk aan: 7.867232338032379 bij p= 1 , d= 1 en q= 3 is RMSE gelijk aan: 7.705863317823244 bij p= 1 , d= 1 en q= 4 is RMSE gelijk aan: 8.009168665003559 bij p= 1 , d= 2 en q= 1 is RMSE gelijk aan: 5.632391691394949 bij p= 1 , d= 2 en q= 2 is RMSE gelijk aan: 5.311938891000537 bij p= 1 , d= 2 en q= 3 is RMSE gelijk aan: 5.5288344912092455 bij p= 1 , d= 2 en q= 4 is RMSE gelijk aan: 6.936329522047111 bij p= 1 , d= 3 en q= 1 is RMSE gelijk aan: 136.46771477704056 bij p= 1 , d= 3 en q= 2 is RMSE gelijk aan: 22.04219204477042 bij p= 1 , d= 3 en q= 3 is RMSE gelijk aan: 22.37837539437825 bij p= 1 , d= 3 en q= 4 is RMSE gelijk aan: 22.041805398932492 bij p= 1 , d= 4 en q= 1 is RMSE gelijk aan: 51.795336931684716 bij p= 1 , d= 4 en q= 2 is RMSE gelijk aan: 593.9874266711241 bij p= 1 , d= 4 en q= 3 is RMSE gelijk aan: 54.63233233305157 bij p= 1 , d= 4 en q= 4 is RMSE gelijk aan: 21.93620705684888 bij p= 2 , d= 1 en q= 1 is RMSE gelijk aan: 7.840173717120843 ............................................................... bij p= 3 , d= 4 en q= 4 is RMSE gelijk aan: 279.67026713349674 bij p= 4 , d= 1 en q= 1 is RMSE gelijk aan: 8.048579542030273 bij p= 4 , d= 1 en q= 2 is RMSE gelijk aan: 7.763727963825087 bij p= 4 , d= 1 en q= 3 is RMSE gelijk aan: 5.919055958042294 bij p= 4 , d= 1 en q= 4 is RMSE gelijk aan: 8.126752514792717 bij p= 4 , d= 2 en q= 1 is RMSE gelijk aan: 7.155611708050894 bij p= 4 , d= 2 en q= 2 is RMSE gelijk aan: 6.860184530438408 bij p= 4 , d= 2 en q= 3 is RMSE gelijk aan: 4.114869475382971 bij p= 4 , d= 2 en q= 4 is RMSE gelijk aan: 5.599633591955198 bij p= 4 , d= 3 en q= 1 is RMSE gelijk aan: 58.12475829874703 bij p= 4 , d= 3 en q= 2 is RMSE gelijk aan: 90.21180524758114 bij p= 4 , d= 3 en q= 3 is RMSE gelijk aan: 3.2528285976010887 bij p= 4 , d= 3 en q= 4 is RMSE gelijk aan: 19.634888387180006 bij p= 4 , d= 4 en q= 1 is RMSE gelijk aan: 2690.867316375142 bij p= 4 , d= 4 en q= 2 is RMSE gelijk aan: 289.1810635224017 bij p= 4 , d= 4 en q= 3 is RMSE gelijk aan: 195.87705789239428 bij p= 4 , d= 4 en q= 4 is RMSE gelijk aan: 513.2304879702396
Wat is de parameter-set van p, d en q met de laagste RMSE?
RMSE_idx = parameters[['RMSE']].idxmin()
print("minimum RMSE bedraagt ", parameters['RMSE'].min(), "bij index :", RMSE_idx)
print("p waarde: ", parameters.loc[RMSE_idx,'P'])
print("d waarde: ", parameters.loc[RMSE_idx,'D'])
print("q waarde: ", parameters.loc[RMSE_idx,'Q'])
print("de minimum RMSE waarde is inderdaad bij de gevonden index waarde:", ((parameters['RMSE'].min() - parameters.loc[RMSE_idx,'RMSE']) == 0))
minimum RMSE bedraagt 3.2528285976010887 bij index : RMSE 58 dtype: int64 p waarde: 58 4 Name: P, dtype: object d waarde: 58 3 Name: D, dtype: object q waarde: 58 3 Name: Q, dtype: object de minimum RMSE waarde is inderdaad bij de gevonden index waarde: 58 True Name: RMSE, dtype: bool
Bij p=4, d=3 en q=3 is de RMSE het laagst, te weten 3,25 °C.
p = int(p)
d = int(d)
q = int(q)
print(p,d,q)
Pas het ARIMA model met de gevonden parameters toe
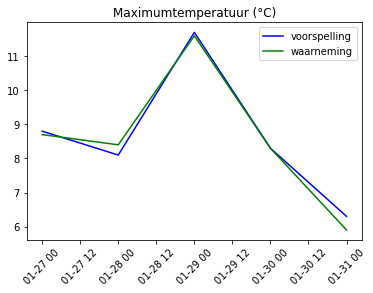
Voorspel de temperatuur over de laatste vijf dagen van januari en vergelijk deze met de gemeten temperatuur.
model3 = ARIMA(df.maximumtemp, order=(p,d,q))
model3 = model3.fit()
#voorspel volgende vier dagen
index_future_dates=pd.date_range(start='27-01-2022', periods=9)
#print(index_future_dates)
pred=round(model3.predict(start=(len(df)-4),end=len(df)+4,typ='levels').rename('voorspelling'),1)
#print(comp_pred)
pred.index=index_future_dates
#print(pred)
waarneming = df.maximumtemp[-5:].astype(float)
#waarneming.reset_index(drop=True, inplace=True)
#print(waarneming)
voorspelling = pred[:5].astype(float)
#print(voorspelling)
w = waarneming.to_frame()
w.reset_index(drop=True, inplace=True)
v = voorspelling.to_frame()
v.reset_index(drop=True, inplace=True)
#print(w,v)
tot = pd.concat([v, w], axis=1).astype(float)
print(tot)
tot = tot.rename(columns={'maximumtemp': 'waarneming'})
print(tot)
print(tot.dtypes)
tot['verschil'] = tot.voorspelling - tot.waarneming
tot['kwadraat_verschil'] = tot['verschil']**2
print(tot.describe())
print(tot)
std = (tot['kwadraat_verschil'].sum()/len(tot))**(0.5)
print("standaarddeviatie van de fout is: ", std)
rmse = math.sqrt(mean_squared_error(waarneming,voorspelling))
print("root mean squared error is: ", rmse)
voorspelling maximumtemp
0 8.8 8.7
1 8.1 8.4
2 11.7 11.6
3 8.3 8.3
4 6.3 5.9
voorspelling waarneming
0 8.8 8.7
1 8.1 8.4
2 11.7 11.6
3 8.3 8.3
4 6.3 5.9
voorspelling float64
waarneming float64
dtype: object
voorspelling waarneming verschil kwadraat_verschil
count 5.00000 5.000000 5.000000 5.000000
mean 8.64000 8.580000 0.060000 0.054000
std 1.95397 2.026573 0.250998 0.069498
min 6.30000 5.900000 -0.300000 0.000000
25% 8.10000 8.300000 0.000000 0.010000
50% 8.30000 8.400000 0.100000 0.010000
75% 8.80000 8.700000 0.100000 0.090000
max 11.70000 11.600000 0.400000 0.160000
voorspelling waarneming verschil kwadraat_verschil
0 8.8 8.7 0.1 0.01
1 8.1 8.4 -0.3 0.09
2 11.7 11.6 0.1 0.01
3 8.3 8.3 0.0 0.00
4 6.3 5.9 0.4 0.16
standaarddeviatie van de fout is: 0.2323790007724451
root mean squared error is: 0.2323790007724451
Met de opgegeven parameters is de gemiddelde afwijking tussen de gemeten en de voorspelde temperatuur 0,23 °C. Dat is niet slecht!
Maak het dataframe netjes
tot['datum'] = pd.date_range('27-01-2022', periods=5, freq='D')
tot.set_index('datum', inplace=True)
print(tot)
Toon de voorspelde en gemeten temperatuur in een grafiek
plt.plot(tot['voorspelling'], color='Blue', label = 'voorspelling')
plt.plot(tot['waarneming'], color='Green', label = 'waarneming')
plt.legend()
plt.title('Maximumtemperatuur (°C)')
plt.xticks(rotation=45)
plt.show
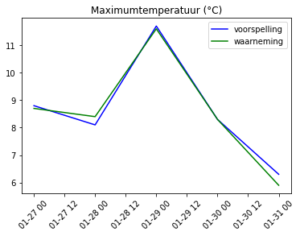
Optimaliseer ARIMA met parameters p, d en q voor de laagste RMSE
Met een beetje spelen met de parameter instellingen komt het ARIMA model best aardig voor de dag. Voorspellingen die dichtbij nu liggen, worden beter door het model opgepakt. Op de lange termijn gaat het model fout. Dat blijkt wel uit de hoge RMSE waarde van meer dan 3 °C.
Er zijn nog andere varianten voor een tijdreeksmodel in python, zoals het SARIMAX model. Dit model neemt behalve het voortschrijdend gemiddelde en de autoregressie component ook een eventueel seizoenspatroon mee in de modellering. Misschien iets voor een volgend bericht. Maar dan moet de tijdreeks wel meerdere jaren omvatten. Nog even wachten met rekenen dus! Wel kunnen we al aan de slag gaan met het auto-ARIMA algoritme. Dit algoritme rekent zelf uit welke parameter-set het beste past. In dit bericht deden we dit nog zelf. Met auto-ARIMA gaat dit vanzelf.