Kloppen de metingen wel?
De metingen worden uitgevoerd met een professioneel weerstation van het merk/type Eurochron EC-4406126. We mogen ervan uitgaan dat in ideale omstandigheden de waarnemingen van de temperatuur, de windsnelheid, luchtdruk, etc. juist zijn. Gekalibreerd onder fabrieksomstandigheden. De praktijk voegt daaraan echter ‘ruis’ toe. Die ontstaat allereerst door de plaatsing. Het weerstation P41_Ermelo is gemonteerd op circa anderhalve meter op een bitumen dak, aan de zijkant van een zonnepaneel.
Wanneer de zon schijnt, warmt het dak snel op. Dit beïnvloedt de temperatuurwaarneming. Het station is redelijk vrij geplaatst ten opzichte van de wind. Alleen vanuit het zuidoosten bevindt het station zich in de luwte van het schuine dak. Hoewel de metingen technisch gezien dus correct zijn, geven deze vermoedelijk een verstoord beeld van de daadwerkelijke situatie door obstakels in de omgeving of het hitte-effect van het dak. Daarom hebben we vrij snel een kalibratie uitgevoerd in februari 2021, twee maanden na ingebruikname van het weerstation. We zullen deze kalibratie na zes maanden herhalen.
KNMI weerstations
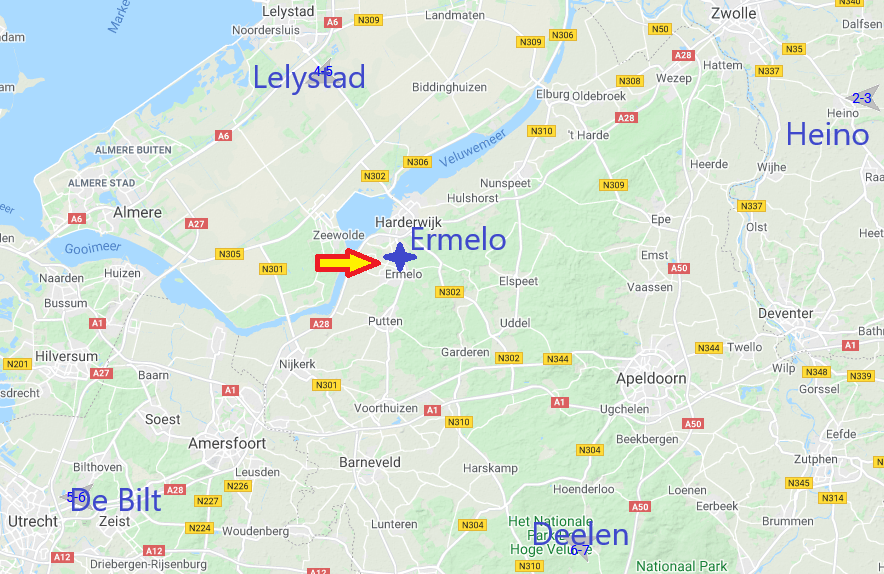
De officiële KNMI weerstations in de nabijheid van Ermelo geven de mogelijkheid om de temperatuurmetingen te kalibreren. Het betreft de stations Lelystad (vliegveld), Heino, Deelen (vliegbasis) en De Bilt.
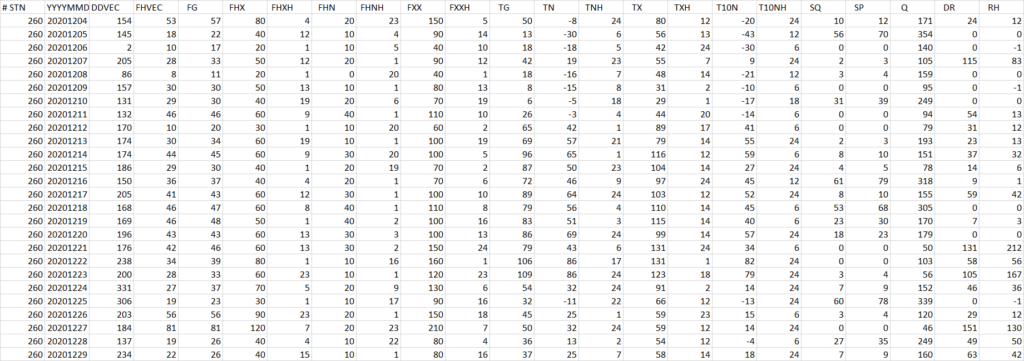
Het KNMI stelt een dataset ter beschikking van de gegevens uit de automatische weerstations. Dat geeft een mogelijkheid om de waarnemingen van P41_Ermelo te kalibreren aan de hand van deze dataset. De gewenste data kun je zelf samenstellen op de KNMI pagina ‘Daggegevens van het weer‘.
Kalibratie
De geselecteerde gegevens resulteren in een datadump in een ASCII format (zie
onderstaande plaatje). Daar is nog niet veel chocola van te maken.
Daarom maken we eerst de data netjes in python met behulp van de pandas
functionaliteit. Het Python pandas package is een open source library met data analyse faciliteiten. Heel handig om inzicht te verkrijgen in de kenmerken van de data, de ‘outliers’, de statistieken en opvallende zaken.
In pandas heb ik dit programma gemaakt om de kalibratie uit te voeren. Het format is in txt opgeslagen. Na download verander je de extensie in .py zodat python of anaconda deze kan inlezen.
De stappen in het programma
- Lees de data van KNMI weerstations in
knmi = pd.read_csv('D:\SynologyDrive\OneDrive\Bart Actueel\Interesse\Python\weer\kalibratie\kal_2\knmi_stations_3.csv', delimiter=';', header=50)
# Verwijder de lege eerste regel onder de kolomnamen
#knmi = knmi.loc[1:,:]
print("hoe ziet dataset eruit?")
print(knmi)
# Verander de datumnotatie naar een integer getal
knmi['YYYYMMDD'] = knmi['YYYYMMDD'].astype(int).round(0)
# Stel de index in op de eerste kolom met de stationsnaam
knmi.set_index("# STN", inplace=True)
print("dataset knmi nadat index op station gesteld is")
print(knmi)
- Verwijder de data die niet nodig zijn, schoon het bestand verder op en print de kerngegevens van de vier KNMI stations
# Selecteer het dataframe met de gewenste kolommen, deel de temperatuurwaarden door 10 en hernoem de kolommen
df = knmi.loc[:, ['YYYYMMDD', ' TG', ' TN', ' TX']]
df[' TG'] = df[' TG']/10
df[' TN'] = df[' TN']/10
df[' TX'] = df[' TX']/10
df.rename({'YYYYMMDD': 'datum', ' TG': 'Tgem', ' TN': 'Tmin', ' TX':'Tmax',}, axis=1, inplace=True)
# Schrijf het dataframe weg onder bestandsnaam xyz
df.to_csv('D:\SynologyDrive\OneDrive\Bart Actueel\Interesse\Python\weer\kalibratie\kal_2\knmi_stations_temp.csv', decimal=',', sep=';')
print("opgeschoond dataframe")
print(df)
# Selecteer de rijen voor station De Bilt (260)
df260 = df.loc['260',:]
df260.set_index("datum", inplace=True)
df260.rename({'Tgem': 'TgemB', 'Tmin': 'TminB', 'Tmax':'TmaxB',}, axis=1, inplace=True)
print("DE BILT")
print(df260)
# Selecteer de rijen voor station Lelystad (269)
df269 = df.loc['269',:]
df269.set_index("datum", inplace=True)
df269.rename({'Tgem': 'TgemL', 'Tmin': 'TminL', 'Tmax':'TmaxL',}, axis=1, inplace=True)
print("LELYSTAD")
print(df269)
# Selecteer de rijen voor station Deelen (275)
df275 = df.loc['275',:]
df275.set_index("datum", inplace=True)
df275.rename({'Tgem': 'TgemD', 'Tmin': 'TminD', 'Tmax':'TmaxD',}, axis=1, inplace=True)
print("DEELEN")
print(df275)
# Selecteer de rijen voor station Heino (278)
df278 = df.loc['278',:]
df278.set_index("datum", inplace=True)
df278.rename({'Tgem': 'TgemH', 'Tmin': 'TminH', 'Tmax':'TmaxH',}, axis=1, inplace=True)
print("HEINO")
print(df278)
# Schrijf de station-dataframes weg onder bestandsnaam xyz
df260.to_csv('D:\SynologyDrive\OneDrive\Bart Actueel\Interesse\Python\weer\kalibratie\kal_2\debilt.csv', decimal=',', sep=';')
df269.to_csv('D:\SynologyDrive\OneDrive\Bart Actueel\Interesse\Python\weer\kalibratie\kal_2\lelystad.csv', decimal=',', sep=';')
df275.to_csv('D:\SynologyDrive\OneDrive\Bart Actueel\Interesse\Python\weer\kalibratie\kal_2\deelen.csv', decimal=',', sep=';')
df278.to_csv('D:\SynologyDrive\OneDrive\Bart Actueel\Interesse\Python\weer\kalibratie\kal_2\heino.csv', decimal=',', sep=';')
# Geef weer wat de gemiddelde temperatuur is van elk station gedurende de meetperiode
print("gemiddelde temperatuur in De Bilt is:", float(df260['TgemB'].mean()))
print("gemiddelde temperatuur in Lelystad is:", float(df269['TgemL'].mean()))
print("gemiddelde temperatuur in Deelen is:", float(df275['TgemD'].mean()))
print("gemiddelde temperatuur in Heino is:", float(df278['TgemH'].mean()))
- Combineer de station-dataframes in een dataframe
kal = pd.concat([df260, df269, df275, df278], axis = 1)
# Haal de index weg en zet de waarden terug als een kolom
kal = kal.reset_index()
print("de shape van het kalibratiebestand is:", kal.shape)
print("toon het kalibratiebestand van de vier KNMI weerstations")
print(kal)
- Haal het bestand op met de weergegevens van station P41_Ermelo, corrigeer de reeds toegepaste off-set van de temperatuur en selecteer alleen de temperatuur
tempgem = pd.read_csv('D:/SynologyDrive/OneDrive/Bart Actueel/Interesse/Python/weer/maandoverzicht/2021/07/tempgem.csv', delimiter=';', decimal=',')
print("toon de gemiddelde temperatuur in P41_Ermelo", tempgem)
# corrigeer voor de reeds toegepaste offset van 0.4°C
print("wat was de eerder gecorrigeerde offset?")
offset = input('geef de offset waarde (inclusief minteken) die in het weerstation is ingevoerd: ')
offset = float(offset)
tempgem.loc[(tempgem.jaar == 2021) & (tempgem.maand > 1),"Tgem"] += -offset
tempgem.loc[(tempgem.jaar == 2021) & (tempgem.maand > 1),"Tmax"] += -offset
tempgem.loc[(tempgem.jaar == 2021) & (tempgem.maand > 1),"Tmin"] += -offset
print("toon de gemiddelde temperatuur in P41_Ermelo zonder offset", tempgem)
# Selecteer alleen de kolommen met temperatuurgegevens
tempgem = tempgem[['Tgem', 'Tmin', 'Tmax']]
tempgem.rename({'Tgem': 'TgemE', 'Tmin': 'TminE', 'Tmax':'TmaxE',}, axis=1, inplace=True)
# Haal de index weg en zet de waarden terug als een kolom (betreft datum)
tempgem = tempgem.reset_index()
# Verwijder de kolom met de datumwaarden
del tempgem['index']
print("de shape van het tempgem P41_Ermelo is:", tempgem.shape)
print("toon kalibratiebestand van P41_Ermelo")
print(tempgem)
- Combineer het dataframe met de temperatuurgegevens van de vier KNMI statinos met het dataframe P41_Ermelo
kal = pd.concat([kal, tempgem], axis = 1)
# Schrijf het nieuwe gecombineerde dataframes weg onder bestandsnaam xyz
kal.to_csv('D:\SynologyDrive\OneDrive\Bart Actueel\Interesse\Python\weer\kalibratie\kal_2\kalibratie.csv', decimal=',', sep=';')
print("toon het gecombineerde kalibratiebestand")
print(kal)
# Geef een indruk van de kenmerken van het dataframe kal
print("Geef een indruk van de kenmerken van het dataframe kal")
print(kal.describe())
- Ons weerstation P41_Ermelo (16m NAP) ligt op de zandgronden van de Veluwe. De karakteristieken van station Deelen, het KNMI station op de Veluwe tussen Apeldoorn en Arnhem, ligt ook op zandgrond (48m NAP). De kalibratie vindt weliswaar plaats op basis van de samengestelde temperatuurgegevens van De Bilt, Lelystad, Deelen en Heino, maar we laten meetstation Deelen iets zwaarder meetellen dan de overige drie stations.
coefficient_Deelen = str(input("geef de weging(%) aan voor station Deelen als percentage (% teken niet noemen) van de vier nabijgelegen stations (Deelen, Lelystad, De Bilt en Heino? "))
coefficient_Deelen = float(coefficient_Deelen) / 100
coefficient_overige = (1 - coefficient_Deelen) / 3
print(coefficient_overige)
# De ijkingsgrootheid betreft de Tagg (Temperatuur, geaggregeerd over de vier stations)
kal['Tagg'] = coefficient_overige * kal['TgemB'] + coefficient_Deelen * kal['TgemD'] + coefficient_overige * kal['TgemH'] + coefficient_overige * kal['TgemL']
print(kal.head())
# Geef een indruk van de correlaties tussen de variabelen.
corrMatrix = kal.corr()
print(corrMatrix)
# Wat is de correlatie tussen de temperatuur van P41_Ermelo (TgemE) en de ijkingstemperatuur (Tagg)?
correlatie = kal["TgemE"].corr(kal["Tagg"])
- Een correlatiecoëfficiënt is een maat voor de correlatie tussen twee stochastische grootheden (of stochastische variabelen). Een correlatiecoëfficiënt +1 of -1 betekent dat er een lineair verband is tussen de beide stochastische variabelen, wat wil zeggen dat de ene variabele volledig uit de andere is te herleiden via een lineaire relatie.
- Een correlatiecoëfficiënt van 0 wil zeggen dat er totaal geen lineaire samenhang is. In de statistiek is een determinatiecoëfficiënt, veelal aangeduid met R², een maat voor het deel van de variabiliteit dat wordt verklaard door het statistisch model. Bij enkelvoudige lineaire regressie is de determinatiecoëfficiënt gelijk aan het kwadraat van een correlatiecoëfficiënt.
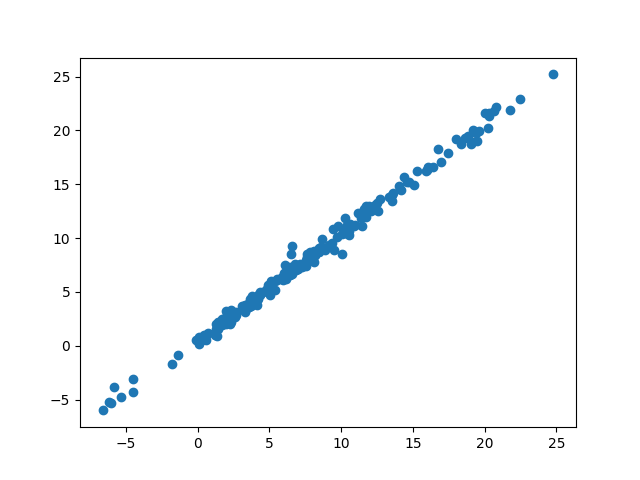
- De correlatiecoëfficiënt bedraagt tussen ons weerstation P41_Ermelo en het geaggregeerde gemiddelde van de vier KNMI weerstations bedraagt 0,998.
- Toon een scatter plot van de samenhang tussen de temperatuur van P41_Ermelo en het geaggregeerde gemiddelde.
- Vind de off-set die aangeeft met hoeveel ºC de temperatuur van P41_Ermelo moet worden bijgesteld.
import numpy as np
# Vind de coëfficiënten van de regressielijn die de punten zo goed mogelijk benadert
# Theta_1 geeft de steilheid van de lineaire functie aan. Aanname: theta_1 is gelijk aan 1.
theta_1 = 1
h = Tagg * theta_1
# Wat is het aantal waarnemingen?
m = len(h)
# Wat is de gemiddelde fout tussen de gemodelleerde lijn (h) en de waarnemingen (TgemE)? (de zogenaamde cost function)
cost = np.sum(((h - TgemE)**2)/(2*m))
# Deze sommatie formule in numpy library sommeert alle waarden in het array (als je bv np.sum(h) doet krijg je het totaal van alle waarden in het h array.)
print("de cost is gelijk aan", cost)
- Pas een offset van 0ºC toe en bepaal de fout tussen de temperatuur van P41_Ermelo en de geaggregeerde temperatuur. De totale afwijking (fout) bedraagt 0,08. Deze is dus heel klein.
- Maar kunnen we nog een betere functie vinden? Hiervoor gebruiken we linear_model schattingsfunctie uit sklearn library.
from sklearn import linear_model
linear = linear_model.LinearRegression()
# Check de vorm van het array van Tagg
print(Tagg.shape)
# Check de vorm van het array van TgemE
print(TgemE.shape)
print("pas in de code aan wat de shape is door deze te reshapen")
# Hervorm de arrays zo dat de linear_model functie ermee kan rekenen.
Tagg = Tagg.values.reshape(209,1)
TgemE = TgemE.values.reshape(209,1)
# Sla het resultaat van de best passende functie op in variabele 'res'.
res = linear.fit(Tagg,TgemE)
# Wat is theta_1 (steilheid) van de lineaire functie?
theta_1 = res.coef_[0][0]
print(theta_1)
# Wat is theta_0 (snijpunt met de y-as) van de lineaire functie?
# Deze waarde geeft aan hoeveel te hoog (of te laag) de gemeten temperatuur (TgemE) ligt ten opzichte van wat je zou verwachten op basis van de vier weerstations.
theta_0 = res.intercept_[0]
print(theta_0)
# Zet de waarden theta_0 en theta_1 in een lineaire functie
model = theta_1*Tagg + theta_0
# Wat is de gemiddelde fout tussen de gemodelleerde lijn (h) en de waarnemingen (TgemE)? (de zogenaamde cost function)
residuals = model - TgemE
print(residuals.shape)
# Toon een scatter diagram en een lijngrafiek van de waarnemingen respectievelijk de gemodelleerde functie
plt.plot(Tagg,TgemE,'b.')
plt.show()
plt.plot(Tagg,model,'-y')
plt.xlabel('Geaggregeerde temperatuur van De Bilt, Deelen, Lelystad, Heino')
plt.ylabel('in °C')
plt.title('Verband tussen geaggregeerde temperatuur en gemeten temperatuur')
plt.show()
# Hoe zijn de afwijkingen verdeeld?
plt.hist(residuals, bins = 20, density=True)
# Hoe meer datapunten worden gebruikt, des te meer de verdeling in het histogram de vorm van een klokkromme (https://nl.wikipedia.org/wiki/Normale_verdeling) krijgt
plt.show()
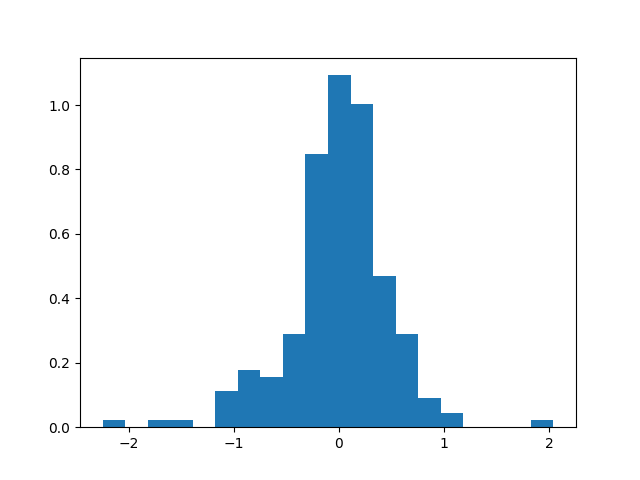
Histogram van de negatieve en positieve afwijkingen
- Te zien is dat er sprake is van een licht positieve afwijking. Het histogram is iets ‘zwaarder’ aan de rechterkant.
- Wat is de gemiddelde fout aan tussen de gemodelleerde lijn (h) en de waarnemingen (TgemE)? (de zogenaamde cost function)?
m = len(residuals)
cost_model = np.sum(((residuals)**2)/(2*m))
print(cost_model)
# Wat is het verschil tussen de cost functie bij aanname theta_1 = 1 en de gemodelleerde functie met theta_0 en theta_1?
verschil = cost - cost_model
print(verschil)
- Bij een verschil is er dus nog verdere verbetering mogelijk geweest door de variabelen theta_0 en theta_1 in te stellen.
- Wat is de ‘offset’ die we op station P41_Ermelo moeten instellen? Dit is gelijk aan de negatieve waarde van theta_0. We veronderstellen dat de steilheid gelijk is aan 1 (deze kunnen en willen we ook niet instellen in het weerstation!).
- Je mag veronderstellen dat het weer in Ermelo altijd even sterk meebeweegt als de andere stations. Zie ook de theta_1 uit het model die gelijk is aan 0.9967501442084191.
theta_1 = 1
- Test voor een honderdtal theta_0 waarden tussen -0.5 en 0.5
reeks = np.linspace(-0.5,0.5,100)
# Maak een lege lijst, output geheten, waarin de totale cost (fout) bij elke gekozen parameter van theta_0, wordt weggeschreven.
output = []
# Bereken de fout (Mean Square Error) voor elke parameter en druk de lijst met MSE-waarden af.
for theta_0 in reeks:
g = theta_0 + Tagg * theta_1
m = len(g)
MSE = np.sum(((g - TgemE)**2)/(2*m))
print("bij een theta_0 van", theta_0, "is de MSE", MSE)
output.append(MSE)
print(output)
# Bepaal bij welke parameterwaarde van theta_0, de totale cost (MSE) het laagst is.
min_value = min(output)
max_value = max(output)
min_index = output.index(min_value)
max_index = output.index(max_value)
print('Index van minimale MSE is: ' + str(min_index))
print('Index van maximale MSE is: ' + str(max_index))
print("De optimale theta_0 (offset P41_Ermelo) is", -0.5 + min_index / 100, "en de cost is", output[min_index])
theta_0 = -0.5 + min_index / 100
print("toon theta_0 ofwel de offset die ik moet invoeren in het weerstation", -1*theta_0)
g = theta_0 + Tagg * theta_1
# Toon de gemodelleerde functie bij de optimale waarde van theta_0.
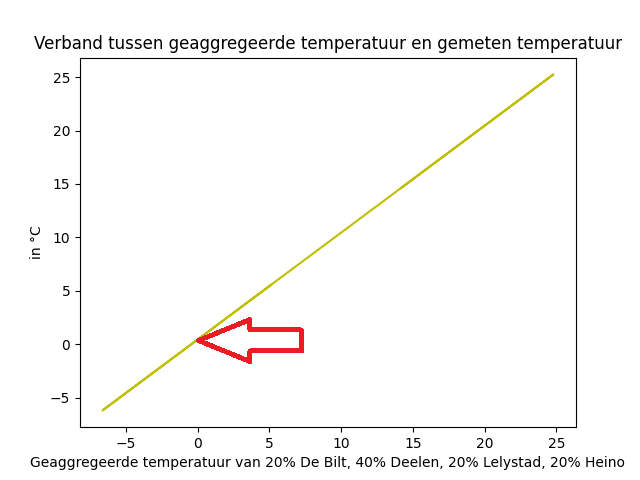
plt.plot(Tagg,g,'-y')
plt.xlabel('Geaggregeerde temperatuur van 20% De Bilt, 40% Deelen, 20% Lelystad, 20% Heino')
plt.ylabel('in °C')
plt.title('Verband tussen geaggregeerde temperatuur en gemeten temperatuur')
plt.show()
- Op basis van twee maanden ijk-data van de vier nabijgelegen KNMI weerstations, komen
we tot de voorlopige conclusie dat de temperatuurwaarnemingen op ons weerstation
P41_Ermelo met -0,28 °C moeten worden bijgesteld, afgerond -0,3 °C. Meer data kun je
lezen in het kalibratiebestand (csv format). - Zoals gezegd zullen we deze kalibratie eens per halfjaar herhalen. Al naar gelang de tijd
verstrijkt, zijn er meer data beschikbaar om de kalibratie op basis van meer data uit te
voeren. Dit zal de betrouwbaarheid van de ijking verbeteren.
Update (7 juli 2021)
- De kalibratie is opnieuw uitgevoerd, nu over het tijdvak dec 2020 – juni 2021. Het blijkt dat
de offset op -0.4 °C uitkomt, wederom op basis van de gewichten zoals deze ook in
voorgaande kalibratie aan de KNMI meetstations zijn toegekend. Ofwel het weerstation
geeft gemiddeld genomen een temperatuur die 0,4 °C hoger ligt dan wat je zou mogen
verwachten. - In het histogram is getoond hoe de verdeling is van de afwijkingen tussen de
gecorrigeerde temperatuur en de ijktemperatuur. Zoals te verwachten zijn de grootste
afwijkingen zeer gering of gelijk aan nul.

De toegepaste data voor deze update herijking zijn opgenomen in bijgaand
kalibratiebestand .