Dit boek van David Sumpter, professor in toegepaste wiskunde, gaat over de 10 wiskundige vergelijkingen die het fundament vormen van de hedendaagse wereld met zijn digitale toepassingen, van investment banking tot gokbedrijven en sociale-mediagiganten. De 10 vergelijkingen geven inzicht hoe je de kans op succes kunt vergroten, hoe je je kunt beschermen tegen financiële verliezen, hoe je gezonder kunt leven en hoe je angstzaaierij kunt doorbreken. Deze zijn echter tot nu toe alleen bekend bij slechts enkelen die de wiskunde achter de digitale technologieën die ons leven beheersen. Sumpter duidt deze groep van enkelen aan als de zogenaamde TEN mensen. Het is geen sociale groep van mensen, maar een verzameling van wetenschappers met inzicht in hoe de formules onze levens beheersen.
Met humor en duidelijkheid laat Sumpter zien dat het niet de technische details zijn die deze formules zo succesvol maken. Het is meer de manier waarop deze formules het mogelijk maken om uitdagingen of problemen vanuit een andere invalshoek te bekijken. De formules zijn eenvoudig en drukken in de kern uit wat het achterliggende principe is. Dat maakt dat het boek ook voor de lezer met weinig wiskunde kennis toch goed leesbaar is.
Wat in ons leven toevallig en onvoorspelbaar lijkt, is de uitkomst van een algoritme dat opgebouwd is uit logica en de 10 wiskundige vergelijkingen. Denk bijvoorbeeld aan de wijze waarop de aanbevelingen voor je worden samengesteld in Netflix of hoe worden de funnel in YouTube wordt opgebouwd. Dit boek toont de toepassing van de wiskunde in de technologieën die we in ons dagelijkse leven ervaren en gebruiken.
-
-
-
-
-
The Betting Equation
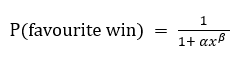
x = de bookmaker’s odds (de notering van de winstkans).Met de parameters α en β kan de notering(de kans van de favourite win) zo worden aangepast dat deze het beste overeenkomst met de realisatie. Je kunt hiervoor het algoritme van logistische regressie inzetten.
De Betting Equation wordt toegepast in neurale netwerkmodellen wanneer een extern signaal (van andere neuronen) moet worden omgezet in een beslissing wat de output is. -
The Judgement Equation
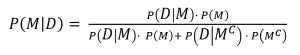
P(M|D) = de kans dat hypothese M waar is gegeven de kans dat de (betreffende) gebeurtenis P(D) zich voordoet.
P(M) = de kans dat hypothese M waar is.
P(D|M) = de kans dat de gebeurtenis zich voordoet gegeven dat de hypothese M waar is.
P(D|Mc) = de kans dat de gebeurtenis zich voordoet gegeven dat de hypothese M niet waar is (tegenovergestelde).
P(Mc) = de kans dat de hypothese niet waar is.Zie onderwerp Bayesiaanse kansrekening.
De Judgement Equation komt van pas bij neurale netwerkmodellen bij het oplossen van vraagstukken met onzekerheid over de aannames. -
The Confidence Equation
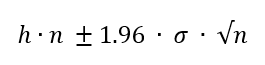
h = verwachtingswaarde
n = aantal trekkingen.
σ = standaarddeviatie.
Zie onderwerp Betrouwbaarheidsinterval.
De Confidence Equation wordt o.a. toegepast bij het bepalen van de tijd die nodig is om een netwerk te trainen om voldoende vertrouwen te hebben dat het netwerkmodel een adequate prestatie heeft. -
The Skill Equation
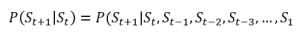
P(St+1|St) = de kans op toestand St+1 gegeven de de toestand St op moment t.
Zie onderwerp Markov eigenschap.
De Skill Equation wordt toegepast in deep learning algoritmen bij het bepalen van de strategie op basis van de huidige toestand zonder rekening te houden met wat er voorafgaand gebeurd is. -
The Influencer Equation
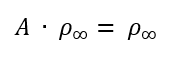
A = de connectiviteitsmatrix die de verbindingen weergeeft tussen personen.
ρ = de vector die de kans weergeeft op het aantal volgers van een persoon (of de omvang van iets/iemand).
De Influencer Equation wordt toegepast bij het inzichtelijk maken van de connecties tussen knopen in netwerken. -
The Market Equation
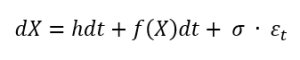
X = de mate van interesse of belangstelling in iets.
dX = de delta in X.
h = het signaal, de mate waarin de interesse wijzigt als functie van de tijd dT.
f(X) = de feedback, de mate waarin het signaal beïnvloed wordt door kuddegedrag.
σ = een maat voor de standaarddeviatie of ‘noise’ waarmee verstoringen van de concurrentie worden aangeduid.
εt = willekeurige afwijking (randomness) die jaarlijks voorkomt.
De Market Equation wordt net als vergelijking 3 toegepast bij het trainen van netwerkmodellen. De vergelijking leert om dieper te graven in het marktsentiment rondom een product (of trend) door drie drijvers uit elkaar te rafelen: het signaal, de feedback en de verstoringen. -
The Advertising Equation
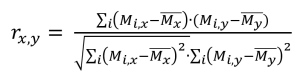
r = de correlatie tussen verschillende variabelen.
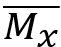
De Advertising Equation vormt de grondslag voor de methode van unsupervised learning waarmee patronen of kenmerken in data worden bepaald. -
The Reward Equation
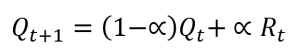
Rt = de beloning (een like of een kudo).
α = de mate waarin de inschatting degradeert bij het uitblijven van een beloning.
De Reward Equation wordt toegepast om te convergeren naar de beste strategie, aan de hand van beloningen. -
The Learning Equation
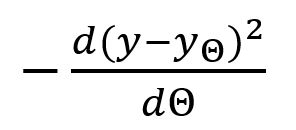
Θ = (aanpasbare) parameter waarmee een neuron de relatie ‘encodeert’ van een relatie tussen een input en output.
y = de waargenomen waarde van variabele y
yΘ = de voorspelde waarde van variabele y
Door het zodanig aanpassen van parameter Θ dat de afstand tussen de waargenomen en voorspelde waarde afneemt, wordt de optimale waarden van Θ verkregen. Dit gebeurt bij positieve waarden van de breuk. Het geleidelijk verhogen van Θ tot het optimum wordt ook gradient ascent genoemd.
De Learning Equation wordt toegepast in machine learning. Het neurale netwerk leert steeds betere voorspellingen te maken. -
The Universal Equation
If…. then….
Sumpter sluit af met een hoofdstuk over de universele vergelijking ‘if… then’ die hij als een afkorting ziet voor alle algoritmen die geschreven kunnen worden als een serie ‘if… then’ statement en ‘repeat… until’ loops. ‘If… then’ logica geeft altijd het juiste antwoord. Wiskunde is rigoreus en waar. Ook al bevalt de waarheid niet altijd, van een moreel gezichtspunt.
-
-
-
-
Het boek is verkrijgbaar in de boekhandel.
